- Из Википедии, свободной энциклопедии в математическая логика Теоремы Гёделя о неполноте являются...
- Примеры неразрешимых утверждений [ редактировать ]
- Недоразумения вокруг теорем Гёделя [ редактировать ]
- Обсуждение и последствия [ редактировать ]
- Набросок доказательства первой теоремы [ редактировать ]
- Набросок доказательства второй теоремы [ редактировать ]
- Смотрите также [ редактировать ]
Из Википедии, свободной энциклопедии
в математическая логика Теоремы Гёделя о неполноте являются двумя известными теоремами Курт Гёдель в 1930 , Упрощенно, первая теорема утверждает:
В любой формализации последовательный математики, которая достаточно сильна, чтобы определить понятие натуральные числа может быть построено утверждение, которое нельзя ни продемонстрировать, ни опровергнуть в рамках этой системы.
Эта теорема является одной из самых известных за пределами математики и одной из самых плохо понятых. Это теорема в формальной логике , и как таковую ее легко интерпретировать. Есть много утверждений, которые кажутся похожими на эту первую теорему Гёделя о неполноте, но в действительности они не соответствуют действительности. Это обсуждается в Недоразумения вокруг теорем Гёделя ,
Вторая теорема о неполноте Гёделя, которая демонстрируется формализующей частью доказательства первой теоремы в пределах собственной системы, утверждает:
Никакая последовательная система не может быть использована для доказательства себя.
Этот результат был разрушительным для философского подхода к математике, известного как формализация программы Гильберта , Дэвид Хилберт Предполагается, что согласованность более сложных систем, таких как реальный анализ , это может быть доказано в терминах более простых систем. Наконец, согласованность всей математики может быть сведена к базовой арифметике. Вторая теорема Гёделя о неполноте показывает, что базовая арифметика не может быть использована для демонстрации собственной согласованности и, следовательно, не может продемонстрировать согласованность чего-либо более сильного.
//
Значение теорем Геделя [ редактировать ]
Теоремы Гёделя - это теоремы в логика первого порядка и должны быть поняты в этом контексте. В формальной логике и математические утверждения, и демонстрации написаны на символическом языке, на котором достоверность тестов может быть проверена механически. Таким образом, не может быть никаких сомнений в том, что теорема выводится из нашего первоначального списка аксиом. Теоретически, этот тип тестов может быть проверен с помощью компьютера, и на самом деле есть программы, которые делают это (это называется автоматическое рассуждение ).
Чтобы выполнить этот процесс, вам нужно знать, что это за аксиомы. Вы можете начать с конечного набора аксиом, как в Евклидова геометрия или, в более общем смысле, можно разрешить бесконечное количество аксиом с требованием, чтобы при условии подтверждения оно могло быть проверено механически, если это одна из аксиом. Хотя может показаться странным использовать бесконечное количество аксиом, это именно то, что обычно делается с натуральными числами, Аксиомы Пеано ,
Первая теорема Гёделя о неполноте показывает, что любая система, которая допускает определение натуральных чисел, обязательно является неполной: она содержит утверждения, которые нельзя ни доказать, ни опровергнуть.
Существование неполной системы само по себе не особенно удивительно. Например, если постулат о параллелизме Евклидова геометрия Вы получаете неполную систему. Неполная система может просто означать, что все необходимые аксиомы не были обнаружены.
Гедель показал, что в большинстве случаев, как в теория чисел или в реальный анализ Вы никогда не сможете обнаружить полный набор аксиом. Каждый раз, когда добавляется новая аксиома, всегда будет недоступна другая.
Вы также можете добавить бесконечный набор аксиом. Например, все истинные утверждения о натуральных числах , но этот список не будет рекурсивный набор , Учитывая любое утверждение, не будет никакого способа узнать, является ли это аксиомой в системе или нет. При наличии теста в общем случае не будет способа проверить, является ли доказательство действительным.
Теорема Геделя имеет другую интерпретацию в контексте информатики. В логике первого порядка теоремы рекурсивно перечислимый : вы можете создать компьютерную программу, которая в конечном итоге даст действительную демонстрацию. Однако они не выполняют самое сильное свойство быть рекурсивным набором: вы не можете создать программу, которая, учитывая подтверждение, определяет, является ли она истинной или нет.
Многие логики считают, что теоремы Гёделя о неполноте нанесли смертельный удар Программа формализации Гильберта это указывало на универсальный математический формализм. Общепринятая позиция состоит в том, что это была вторая теорема, которая нанесла этот удар. Некоторые, однако, думают, что это было первым, и есть даже те, кто считает, что никто из них этого не сделал.
Примеры неразрешимых утверждений [ редактировать ]
Существование неразрешимого утверждения в формальной системе само по себе не является удивительным явлением.
Последующая совместная работа Геделя и Пол Коэн дал конкретные примеры неразрешимых утверждений: оба аксиома выбора как гипотеза континуума неразрешимы в стандартной аксиоматизации теория множеств , Эти результаты не требуют теоремы о неполноте.
в 1936 , Алан Тьюринг показал, что остановить проблему (вопрос о том, Машина Тьюринга остановится при вводе некоторых данных) неразрешима. Позднее этот результат был обобщен в области рекурсивные функции в Теорема Райса это показывает, что все проблемы решения, которые не являются тривиальными, неразрешимы в системе, полной по Тьюрингу.
в 1973 было показано, что Уайтхед проблема в теория групп это неразрешимо в стандартной теории групп. в 1977 Кирби, Париж и Харрингон продемонстрировали, что утверждение в комбинаторный версия Теорема Рэмси , неразрешима в аксиоматизации арифметики, заданной Аксиомы Пеано но это может быть доказано в более широкой системе теории множеств. Алгоритм Крускала , что имеет значение в информатике, также неразрешимо из аксиом Пеано, но демонстрируется в теории множеств. Кроме того, Теорема Гудштейна это относительно простое утверждение о натуральных числах, которое неразрешимо в арифметике Пеано.
Григорий Чайтин предъявил неразрешимые претензии в Алгоритмическая теория информации и фактически он продемонстрировал свою собственную теорему о неполноте в этом контексте.
Одна из первых проблем, которые, как подозревали, были неразрешимы, была проблема эквивалентности утверждений о группах , первоначально предложенный Макс Ден в 1911 , который устанавливает, что есть группа представлены конечным образом, для которого не существует алгоритма, который решает, эквивалентны ли две формулы, которые говорят только о свойствах этих групп. Неразрешимая природа этого утверждения не была продемонстрирована до 1952 ,
Недоразумения вокруг теорем Гёделя [ редактировать ]
Поскольку первая теорема Гёделя о неполноте настолько известна, она породила множество недоразумений. Здесь мы суммируем некоторые:
- Теорема не подразумевает, что любая интересная аксиоматическая система неполна. Например, Евклидова геометрия это может быть аксиоматизировано, так что это целая система. (На самом деле, оригинальные аксиомы Евклид они почти полная аксиоматизация. Отсутствующие аксиомы выражают свойства, которые кажутся настолько очевидными, что было необходимо появление идеи формального доказательства, пока они не были пропущены.) Однако даже в полной системе, такой как геометрия, будут невозможные конструкции ( угловая трисекция , квадрат круга ).
- Теорема применима только к системам, которые позволяют определять натуральные числа в целом. Недостаточно, чтобы система содержала натуральные числа. Он также должен уметь выражать понятие « x - натуральное число», используя аксиомы и логику первого порядка. Есть много систем, которые содержат натуральные числа и являются полными. Например, оба реальные цифры как комплексные числа у них есть полная аксиоматизация.
Обсуждение и последствия [ редактировать ]
Результаты незавершенности влияют на философия математики особенно в отношении таких точек зрения, как формализм , который использует формальную логику для определения своих принципов. Вы можете перефразировать первую теорему, сказав: «Вы никогда не сможете найти аксиоматическую систему, которая способна продемонстрировать все математические истины и никакой лжи».
С другой стороны, со строго формалистической точки зрения этот парафраз будет считаться бессмысленным, поскольку он предполагает, что математическая «истина» и «ложность» четко определены в абсолютном смысле, а не относительно каждой формальной системы.
Следующая переформулировка второй теоремы еще более тревожит основы математики:
Если можно показать, что аксиоматическая система является последовательной от самой себя, то она противоречива.
Поэтому, чтобы установить согласованность системы S , необходимо использовать другую систему T , но T- тест не является полностью убедительным, если только согласованность T не была проверена без использования S. Последовательность Аксиомы Пеано для натуральные числа например, это может быть продемонстрировано в теория множеств , но не только в теории натуральных чисел. Это дает отрицательный ответ на проблему номер два из известного списка важных открытых вопросов по математике Дэвид Хилберт (так называемый Проблемы Гильберта ).
В принципе, теоремы Гёделя все еще оставляют некоторую надежду: возможно, алгоритм В общем, для данного утверждения определите, является ли оно неразрешимым или нет, что позволяет математикам полностью избежать неразрешимых проблем. Тем не менее, отрицательный ответ на проблема разрешения показывает, что такого алгоритма нет.
Следует отметить, что теоремы Гёделя применимы только к достаточно сильным аксиоматическим системам. Этот термин означает, что теория содержит достаточную арифметику для выполнения инструкций по кодированию, необходимых для доказательства первой теоремы о неполноте. По сути, все, что требуется, это некоторые основные факты о сложении и умножении, как, например, они формализованы в арифметика Q Робинсона , Есть даже более слабые аксиоматические системы, которые являются последовательными и полными, например, арифметика Пресбургера который показывает все истинные утверждения первого порядка, применяя только сумму.
Аксиоматическая система может состоять из бесконечного числа аксиом (как это делает арифметика Пеано первого порядка), но для того, чтобы применить теорему Геделя, должен существовать эффективный алгоритм, способный проверить правильность тестов. Например, набор всех операторов первого порядка, которые являются истинными в стандартной модели натуральные числа Это завершено. Теорема Геделя не может быть применена, потому что нет эффективной процедуры, которая решает, является ли определенное утверждение аксиомой. Фактически это является следствием первой теоремы Гёделя о неполноте.
Другой пример спецификации теории, в которой первая теорема Гёделя неприменима, может быть построен следующим образом: мы упорядочиваем все возможные утверждения о натуральных числах сначала по их длине, а затем в лексикографический порядок ; давайте начнем с аксиоматической системы, изначально равной аксиомам Пеано, рассмотрим список утверждений один за другим и, если текущее утверждение не может быть доказано или опровергнуто из текущей системы аксиом, добавьте его в список. Это создает систему, которая является полной, последовательной и достаточно мощной, но не рекурсивно перечислимый ,
Сам Гедель доказал лишь версию приведенных выше теорем, которая технически немного слабее; Первая демонстрация версий, описанных выше, была дана Дж. Баркли Россер в 1936 ,
По сути, доказательство первой теоремы состоит в том, чтобы построить утверждение р в формальной аксиоматической системе, которой может быть дана следующая математическая цель:
p
= «Это утверждение не может быть доказано.»
Таким образом, это можно рассматривать как современную версию Лжец парадокс , Вопреки утверждению лжеца, р не ссылается непосредственно на себя; приведенная выше интерпретация может быть «видна» только снаружи формальной системы.
В работе, опубликованной в 1957 году в журнале символической логики , Раймонд Смуллян показали, что результаты неполноты Гёделя могут быть получены для гораздо более элементарных систем, чем те, которые рассматривал Гёдель. Смуллян также претендовал на самые простые тесты с той же областью, основанные на работах Альфред Тарский о понятии истины в формальных системах. Проще, но не менее тревожно с философской точки зрения. Смуллян не отразил свои размышления о незавершенности только в технических работах; Они также вдохновили известные популярные книги, такие как « Как называется эта книга»? ,
Если аксиоматическая система непротиворечива, доказательство Геделя показывает, что p (и его отрицание) не могут быть продемонстрированы в системе. Следовательно, p истинно ( p утверждает, что не является доказуемым и не является доказательством) и, однако, не может быть официально доказано в системе. Обратите внимание, что добавление p к аксиомам системы не решило бы проблему: для расширенной теории было бы другое предложение Геделя.
Роджер Пенроуз он утверждает, что эта (предполагаемая) разница между тем, что может быть доказано механически, и тем, что люди могут видеть в качестве определенного образца, показывает, что человеческий интеллект не является механическим по своей природе. также JR Lucas обратился к этому требованию в Умы, Машины и Гедель (на английском).
Эта точка зрения не является общепринятой, потому что она возникает Марвин Минский человеческий интеллект способен ошибаться и понимать утверждения, которые на самом деле противоречивы или ложны. Тем не менее, Минский сообщил, что Курт Гёдель он сказал ему лично, что он верит, что у людей есть интуитивный, а не только вычислительный способ достижения истины, и поэтому их теорема не ограничивает то, что люди могут назвать истиной.
Положение о том, что теорема показывает, что у людей есть навык, превосходящий формальную логику, также может быть подвергнуто критике следующим образом: мы не знаем, верно ли предложение p , потому что мы не знаем (и не можем знать), является ли система последовательны. Таким образом, мы на самом деле не знаем никакой истины, которая находится за пределами системы. Все, что мы знаем, это следующее:
Либо недоказуемо в системе, либо система противоречива.
Это утверждение легко демонстрируется внутри системы .
Еще одним следствием является то, что работа Геделя мотивирована Алан Тьюринг (1912-1954), чтобы изучить, какие функции могут быть рассчитаны, а какие нет. Для этого он использовал его Машина Тьюринга машина общего назначения, с помощью которой формализуются функции и процедуры расчета. Доказательство наличия функций, которые невозможно вычислить с помощью машины Тьюринга. парадигма этого набора функций представляется функцией, которая устанавливает, что «если задана машина Тьюринга, она дает результат или, наоборот, остается вычисленной бесконечно». Эта функция, известная под именем Остановить проблему (Проблема остановки), будет фундаментальной частью, чтобы продемонстрировать несопоставимость определенных функций.
Набросок доказательства первой теоремы [ редактировать ]
Основная проблема в сборке вышеупомянутой демонстрационной идеи заключается в следующем: чтобы построить утверждение p , эквивалентное « p не может быть доказано», p должно будет каким-то образом содержать ссылку на p, которая может привести к регрессии бесконечна. Ниже мы опишем гениальный трюк Геделя, который позже будет использован Алан Тьюринг решить проблема разрешения ,
Начнем с того, что любая формула или утверждение, которое может быть сформулировано в нашей системе, получает уникальный идентификатор, называемый Число Геделя , Это сделано таким образом, что легко механически преобразовать формулы в числа Геделя. Поскольку наша система достаточно сильна, чтобы рассуждать о числах , теперь также можно рассуждать и о формулах .
Формула F ( x ), которая содержит ровно одну свободную переменную x , называется декларативной формой . Как только x заменяется определенным числом, объявление становится объявлением добросовестный и либо демонстрируется в системе, либо нет. Декларативные формы не являются заявлениями и поэтому не могут быть доказаны или опровергнуты. Однако каждая декларативная форма F ( x ) имеет число Гёделя, которое мы будем обозначать как G ( F ). Выбор свободной переменной, выбранной в форме F ( x ), не имеет отношения к присвоению числа Gödel G ( F ).
Внимательно проанализировав аксиомы и правила системы, мы можем написать декларативную форму P ( x ), которая воплощает идею x как числа Геделя утверждения, которое может быть продемонстрировано в нашей системе. Формально: P ( x ) может быть проверено, если x - число Геделя доказуемого утверждения и его отрицание 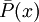 Вы можете попробовать это, если это не так. (Хотя этого достаточно для этой схемы испытаний, технически она не совсем точна - см. Статью Геделя об этой проблеме и статью Россера для ее решения - ключевое слово - омега-согласованность ).
Вы можете попробовать это, если это не так. (Хотя этого достаточно для этой схемы испытаний, технически она не совсем точна - см. Статью Геделя об этой проблеме и статью Россера для ее решения - ключевое слово - омега-согласованность ).
Теперь приходит хитрость: декларативная форма F ( x ) называется само-недоказуемой, если форма F , примененная к собственному числу Гёделя, не демонстрируется. Эта концепция может быть формально определена, и может быть построена декларативная форма S U ( z ), интерпретация которой заключается в том, что z является числом Гёделя декларативной формы, автоопределимой. Формально S U ( z ) определяется как: z = G ( F ) для некоторой конкретной формы F ( x ), а y - число Гёделя объявления F ( G ( F )), и 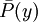 , Теперь желаемое утверждение p , которое было упомянуто ранее, может быть определено как:
, Теперь желаемое утверждение p , которое было упомянуто ранее, может быть определено как:
p
= S U ( G ( S U )).
Интуитивно, когда мы спрашиваем, является ли p истинным, мы спрашиваем: «Является ли это свойство быть самоуничижительным, самодемонстративным?» Это напоминает Парадокс парикмахера о парикмахере, который бреет всех людей в деревне, которые не бреются: бреется ли он сам?
Теперь предположим, что наша аксиоматическая система является последовательной.
Если бы p было доказуемо, то S U ( G ( S U )) было бы истинным, и по определению S U z = G ( S U ) было бы числом Гёделя декларативной авторазличимой формы. Следовательно, S U был бы самодемонстративным, что по определению этого термина подразумевает, что S U ( G ( S U )) не является демонстративным, но это было нашей идеей : а б л е . Это противоречие показывает, что p не может быть доказуемым.
Если бы отрицание p = S U ( G ( S U )) было вероятным, то по определению S U это означало бы, что z = G ( S U ) не является числом Гёделя в само-показательной форме, что подразумевает что S U не является самоограниченным. По определению самоограничения мы заключаем, что S U ( G ( S U )) доказуемо, и, следовательно, p демонстрируемо. Опять противоречие. Это дает понять, что отрицание p также не может быть доказано.
Поэтому утверждение не может быть доказано или опровергнуто в нашей системе.
Набросок доказательства второй теоремы [ редактировать ]
Пусть p будет ранее построенным неразрешимым предложением, и предположим, что согласованность системы может быть проверена в самой системе. Выше мы видели, что если система непротиворечива, то p не показывается. Доказательство этого следствия может быть формализовано в самой системе, и поэтому утверждение " p не является доказуемым" или "нет P ( p )" может быть продемонстрировано в системе.
Но это последнее утверждение эквивалентно самому p (и эта эквивалентность может быть продемонстрирована в системе), поэтому p может быть продемонстрировано в системе. Это противоречие показывает, что система должна быть несовместимой.
Смотрите также [ редактировать ]
Внешние ссылки и ссылки [ редактировать ]
Раймонд Смуллян, теоремы Гёделя о неполноте , издательство Оксфордского университета, 1992 ISBN 0195046722
Ссылки на английском.
Перевод на испанский язык: Курт Гёдель: Полное собрание сочинений . Хесус Мостерин и другие (Trad.) Alianza Редакция, Мадрид (1981). ISBN 8420622869
- Б. Россер: Расширения некоторых теорем Геделя и Черча . Журнал символической логики, 1 (1936), № 1, с. 87-91
- Карлис Подниекс: вокруг теоремы Гёделя , http://www.ltn.lv/~podnieks/gt.html
- Хофштадтер, Дуглас Р. 1979: Гедель, Эшер, Бах: вечная и изящная петля , TusQuets editores, третье издание (1989), Барселона. ISBN 84-7223-459-2
- Эрнест Нагель, Джеймс Рой Ньюман, Дуглас Р. Хофштадтер: Доказательство Гёделя , исправленное издание (2002). ISBN 0814758169 ,
- Вторая проблема Гильберта
- Норберт Домейсен, Логик дер Антиномьен. Берн и др.: Питер Лэнг. 142 с. 1990. ( ISBN 3-261-04214-1 ) Zentralblatt MATH
Ссылки на испанском
Игнасио Джане, Работа Геделя по математической логике и теории множеств Синтетическое и историческое введение, которое уважает оригинальные концепции, избегая недоразумений.
Обзор на испанском Теркель Фразен, теорема Гёделя: неполное руководство по его использованию и злоупотреблению . Книга Францена 2005 года цитируется как интересная работа, чтобы ввести истинный смысл теорем Геделя и предотвратить их неоправданное применение в нематематических областях.








